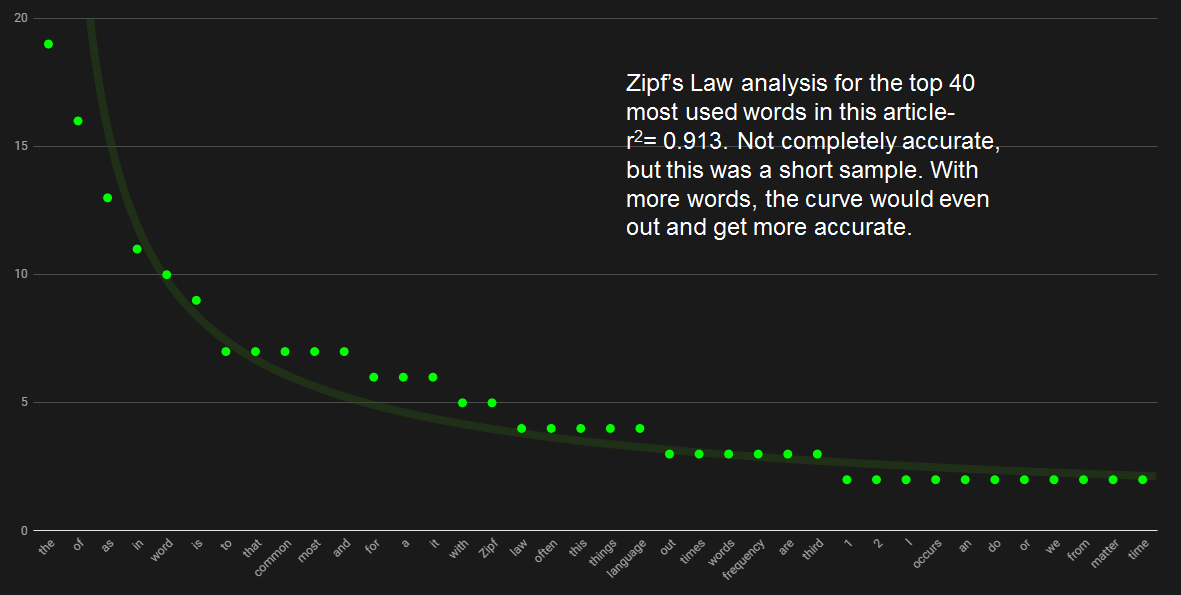
Let this sink in: for any given language, the most common word will occur twice as often as the second most common word, three times as often as the third most common word, and so on (or that the frequency of a word is inversely proportional to its statistical rank such that P(r)=1/[rln(1.78R)], closely enough). This follows a power series regression to reasonably strong correlations for every time. It’s called Zipf’s law and it works!

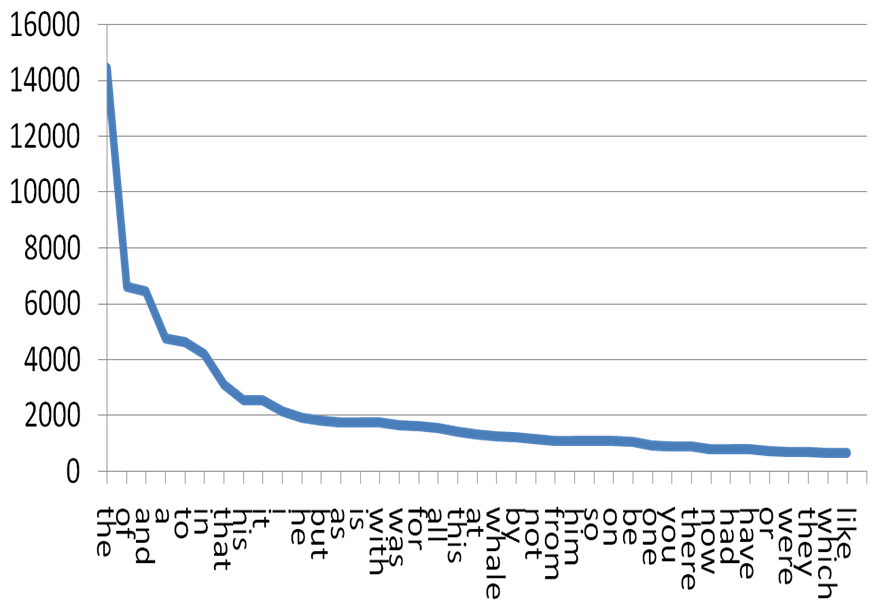
Here’s some proof: the word “the” is the most common word in the English language, with about a 7.0% occurrence out of all words we use. “Of” comes next, with 3.6% of all occurrences. In third, there’s “and” with 2.9%. Therefore, our first most common word occurs 1.94 times as often as the second most common word and 2.41 times as often as the third common word.

Yes, the curve is not perfect. But with hundreds of thousands of words in the English language, it evens out pretty well in the end. As I already emphasized before, this is true for every language, because it’s something that naturally occurs.

And as a naturally occurring phenomenon, Zipf’s Law is true for other things in nature as well. There have been applications from computing to politics. Expressed genes in a cell are Zipfian, as are city population trends, dolphin noises, fortunes of companies, YouTube video views, movie tickets sold, et cetera. Basically, a large number of things that have something to do with popularity or frequency can be shown to follow Zipf’s Law, even though it was just intended for linguistics when it started out.

An interesting thing that comes out of Zipf’s law graphs is the Pareto distribution, in which the top 20% of words are used 80% of the time. And, just as with Zipf’s Law, this principle holds true for many other things in nature, like for Internet traffic, values of oil reserves, city populations, sizes of sand particles, stock price returns, rainfall frequency, and much, much more.

The fact of the matter is that we live in an ordered universe. Mathematical principles govern the most innocuous things, from circle circumferences to decay of matter to apparently dolphin noises. I think that’s incredibly interesting, and  hope you remember how science is in everything you do.